Skip to main content

Rechnen mit Python

Python Compiler

Kürzen eines Bruchs

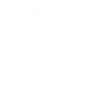
Programmiere mit Python ein Programm, das einen Bruch (rationale Zahl) kürzt. Dazu benötigt man den ggT: Hier ist der Algorithmus für den ggT: 

ggT.drawio.png

Dann muss der Zähler und Nenner nur noch durch den ggT geteilt werden. Das benötigt ihr dazu: Die Informationen gibt es im Unterricht. Hier ist das Grundgerüst für dein Programm: 

def ggt(x,y):
    """
    Die Funktion berechnet den größten gemeinsamen Teiler aus den beiden
    Parametern x und y.
    """
    while x!=y:
        #Dein Code
    return x

def kuerzen(x,y):
    """
    Diese Funktion kürzt den Bruch x/y:
    """
    g=ggt(x,y)
    #Dein Code
    ergebnis= str(int(x))+ '/'+ str(int(y))
    return ergebnis

print ("Der Bruch lautet gekürzt: ", kuerzen(65,135))

Fakultät

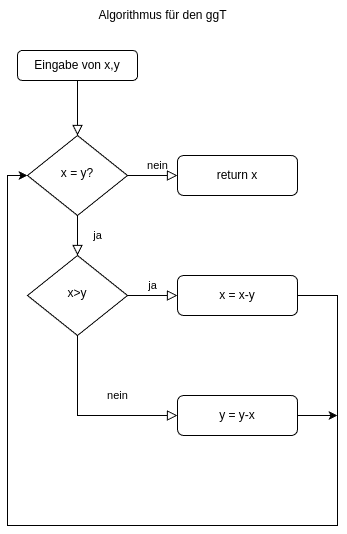
Als nächstes berechnen wir die Fakultät. ACHTUNG: Zum Ausprobieren wählt keine großen Zahlen, da der Rechner schnell überfordert sein wird. Die Fakultät ist folgendermaßen definiert:

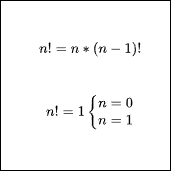
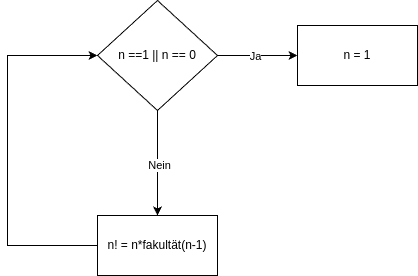
Um das zu berechnen, können wir einfach folgenden Algorithmus verwenden:

Fibonacci-Folge

Für diejenigen, die schnell fertig sind, gibt es noch die Fibonaccifolge, die folgendermaßen definiert ist: 0,1,1,2,3,5,8,13… . Na, wie geht es wohl weiter?

Ackermann-Funktion

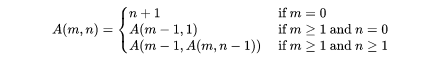
Die Ackermann-Funktion gilt nur für Ganzzahlen >=0!

Folgendermaßen kann diese Funktion umgesetzt werden:

#### Die Ackermann-Funktion, umgesetzt in Python
import sys
sys.setrecursionlimit(10000) # Das Limit für Rekursion in Python ist 1000. Das ist schnell erreicht.

def ackermann(m,n):
  # Für den ersten Fall, dass m=0 ist, wird das Ergebnis n+1 zurückgegeben.
  # Schreibe hier deinen Code für diesen Fall.

  # Für den zweiten Fall, dass m>=1 und n=0 ist, wird als Ergebnis der erneute Aufruf der Funktion übergeben mit den beiden Parametern: ackermann(m-1,1)
  # Schreibe hier den Code für diesen Fall.

  # Für den dritten Fall gilt, dass m und n >= 1 sind. In diesem Fall ist das Ergebnis ackermann(m-1, ackermann(m,n-1))
  Schreibe hier deinen Code für den dritten Fall.

Teste zunächst mit Zahlen <=4!!

Back to top